Das Sortieren von Listen ist eine häufige Aufgabe in der Programmierung. Es lässt sich sehr gut mit Papier und Stift nachvollziehen und daher auch für Newbies geeignet.
Ein Sortieralgorithmus sorgt dafür, dass eine Liste nach einem bestimmten Kriterium sortiert wird. Wichtig ist, dass sich die Elemente eindeutig sortieren lassen (strenge schwache Ordnung). Das ist bspw. bei Zahlen oder Buchstaben möglich.
sort(["b", "c", "a"]) == ["a", "b", "c"]
sort([3, 1, 2]) == [1, 2, 3]
list = [
{id: 3, n: "b"}, {id: 1, n: "c"}, {id: 2, n: "a"}
]
sortById(list) = [
{id: 1, n: "c"}, {id: 2, n: "a"}, {id: 3, n: "b"}
]
sortByName(list) = [
{id: 2, n: "a"}, {id: 3, n: "b"}, {id: 1, n: "c"}
]
Eigenschaften
Sortierverfahren lassen sich in verschiedene Kategorien einteilen. Ein Unterscheidungsmerkmal ist beispielsweise, ob die Liste selbst direkt verändert (in-place) oder eine sortierte Kopie zurückgegeben wird (out-of-place).
// in-place
list = [1, 2, 3];
sortedList = sort(list);
list == sortedList;Damit hängt auch die Platzkomplexität [1]https://www.studytonight.com/data-structures/space-complexity-of-algorithms zusammen, also eine Aussage, wie viel Speicherplatz für die Sortierung benötigt wird. Das ist in Systemen relevant, wo Speicher eine sehr begrenzte Ressource ist. Des Weiteren ist die Zeitkomplexität (Anzahl der Operationen [2]https://www.studytonight.com/data-structures/time-complexity-of-algorithms) ein wichtiges Kriterium, weil es Aussagen über die Laufzeit ermöglicht.
Komplexität wird üblicherweise in der Landau-Notation (O-Notation [3]https://en.wikipedia.org/wiki/Big_O_notation) angegeben und beschreibt diese im Verhältnis zur Größe der Liste (n [4]https://www.happycoders.eu/de/algorithmen/o-notation-zeitkomplexitaet/). Häufig ist die Laufzeit auch von der initialen Anordnung der Werte abhängig (adaptiv). Es wird zwischen Best-, Average- und Worst-Case unterschieden.
Eine weitere Eigenschaft ist Stabilität. Eine Sortierung-Algorithmus ist stabil, wenn sich die Reihenfolge gleicher Element nach der Sortierung nicht verändert hat.
// stable
sort([1, 2, 3, 2, 2]) = [1, 2, 2, 2, 3]
// unstable
sort([1, 2, 3, 2, 2]) = [1, 2, 2, 2, 3] Naiver Ansatz
Wie sortiert man also eine Liste? Ein erster Gedanke wäre, das Minimum zu suchen und dieses an den Anfang zu verschieben. Dieser Ansatz wird auch Selectionsort[5]https://www.studytonight.com/data-structures/selection-sorting genannt. Dann das nächst größere Minimum und so weiter. Eine Herausforderung sind hierbei doppelte Werte in der Liste.
[3, 1, 2] => min: 1
[1, 3, 2] => min: 2
[1, 2, 3] => min: 3Das weitaus größere Problem ist die Komplexität. Je nach Implementierung, muss die Liste pro Element ein mal komplett durchlaufen werden (Zeit O(n²), in-place). Zudem lässt sich der Ansatz nicht parallelisieren.
Ein weiteres „natürliches“ Vorgehen stellt der sogenannte Insertionsort [6]https://de.wikipedia.org/wiki/Insertionsort dar. Er lässt sich am einfachsten mit einem Kartenspiel beschreiben. Man stelle sich Spielkarten bestehend aus Zahlen vor. Um diese zu sortieren, wird eine Karte entnommen und an der richtigen Stelle eingefügt. Wird der Vorgang wiederholt ist das Blatt am Ende sortiert.
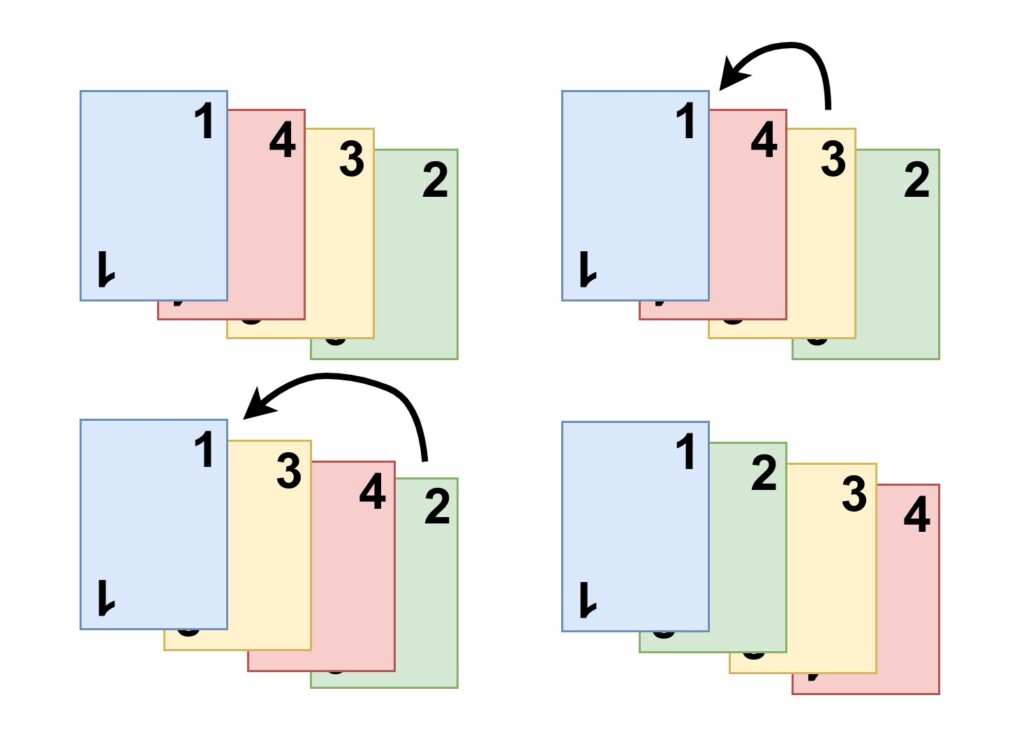
Auch beträgt die Komplexität im Durchschnitt und Wort-Case bei O(n²). Allerdings existieren Optimierungen um die Laufzeit etwas zu verbessern.
Das geht doch besser?
Ja, das stimmt. Bereits 1945 stellte John von Neumann (Neumann-Architektur [7]https://de.wikipedia.org/wiki/John_von_Neumann) den sogenannten Mergesort[8]https://de.wikipedia.org/wiki/Mergesort vor. Bis heute wird Grundprinzip in vielen Programmiersprachen in den eingebauten Sortierfunktionen eingesetzt. Beispielsweise in java.util.List#sort [9]https://docs.oracle.com/javase/8/docs/api/java/util/List.html#sort-java.util.Comparator- oder in Python [10]https://svn.python.org/projects/python/trunk/Objects/listsort.txt. Der Algorithmus wurde allerdings weiterentwickelt und optimiert (Timsort [11] https://de.wikipedia.org/wiki/Timsort).
MergeSort ist ein stabiler Sortieralgorithmus, der das sogenannten Teile-und-Herrsche-Prinzip (Divide-and-Conquer) umsetzt. Hiebei wird die zu sortierende Liste immer wieder geteilt, bis nur noch ein Element vorhanden ist. Beim zusammenführen (merge) wird im Reißverschlussverfahren sortiert. Durch diesen „Trick“ verkürzt sich die Komplexität auf O(n * log(n)). Dabei ist der Teilungsschritt logarithmisch und das Zusammenführen linear. Die Komplexität ist unabhängig von den Eingabedaten (nicht-adaptiv) und gilt somit im Best-, Average- und Worst-Case.

Das Ganze nochmal mit konkreten Werten. Die Liste wird stur in der Mitte geteilt, bis die Teilliste die Länge 1 erreicht hat. Beim Zusammenführen werden die beiden Teillisten dann sortiert. Das geschieht so lange bis die Liste wieder komplett ist.

Die Implementierung kann sehr einfach sein und ist, trotz Rekursion, gut verständlich. Fangen wir mit dem Teilungsschritt an. In Zeile 3 ist die Abbruchbedingung definiert und die Teilung wird beendet. Die Mitte middle der Liste list (Zeile 7) definiert die linke (left) und rechte (right) Teilliste, für wiederum rekursiv mergeSort aufgerufen wird. Wenn diese wieder Aufrufe beendet wurden, geht es in Zeile 11 weiter zum Merge-Schritt. newSubList ist eine Hilfsfunktion um eine Teilliste zu erstellen.
private List<T> mergeSort(final List<T> list) {
final int size = list.size();
if (size <= 1) {
return list;
}
final int middle = size / 2;
final List<T> left = mergeSort(newSublist(list, 0, middle));
final List<T> right = mergeSort(newSublist(list, middle, list.size()));
return merge(left, right);
}Die beiden reingereichten Teillisten werden durchlaufen (Zeile 3 – 9) und die Elemente je nach Größe in eine neue Liste einsortiert (add, Zeile 5 und 7). Vorher werden sie aus den ursprünglichen Teillisten entfernt (remove, Zeile 5 und 7) Sobald eine der beiden Listen leer ist, wird abgebrochen und die neue Liste (mergedList) mit restlichen Elementen der anderen Liste aufgefüllt. Durch die Rekursion wird dieser Schritt auf jeder Ebene ausgeführt und die Teillisten werden immer größer, bis am Ende eine sortierte Liste der ursprünglichen Länge besteht. Durch das regelmäßige Teilen und die Bedingung in Zeile 4, bleibt die Reihenfolge stabil.
private List<T> merge(final List<T> left, final List<T> right) {
final List<T> mergedList = new ArrayList<>();
while (!left.isEmpty() && !right.isEmpty()) {
if (lte(left.get(0), right.get(0))) {
mergedList.add(left.remove(0));
} else {
mergedList.add(right.remove(0));
}
}
mergedList.addAll(left);
mergedList.addAll(right);
return mergedList;
}Die Grundidee des Mergesort ist weiterhin aktuell, auch wenn es mittlerweile einige Optimierungsideen gab. Im Falle der Java- und Python-Implementierung (Timsort), wurde er mit dem Insertionsort kombiniert.
Sonst noch was?
Das Teile-und-Herrsche-Prinzip (insbesondere der Mergesort) lässt sich sehr gut parallelisieren, weil die Teillisten unabhängig verarbeitet werden können. In verschiedensten Implementierungen kann die Laufzeit dadurch noch einmal verbessert werden.
Neben dem Mergesort gibt es eine große Vielfalt an weiteren Sortierverfahren. Dazu zählen beispielsweise Quicksort[12]https://de.wikipedia.org/wiki/Quicksort, Heapsort[13]https://de.wikipedia.org/wiki/Heapsort oder Bubblesort[14]https://de.wikipedia.org/wiki/Bubblesort. Quicksort wurde ~1960 von C. Antony R. Hoare[15]https://de.wikipedia.org/wiki/Tony_Hoare entwickelt und ist ebenso ein Divide-and-Conquer-Algorithmus. Er führt die Sortierung allerdings schon im Teilungsschritt durch und kann bei ungünstigen Eingabewerten eine Komplexität von O(n²) erreichen. Zur selben Zeit wurde auch der Heapsort vorgestellt. Er arbeitet mit einem binären Heap (Binärbaum) und ist ebenfalls sehr effizient (O(n * log(n))).
Ein weiterer Aspekt ist die Kombination verschiedener Sortierverfahren. Der bereits erwähnte Timsort kombiniert beispielsweise Mergsort und Insertionsort. Ähnlich ist es beim Introsort[16]https://de.wikipedia.org/wiki/Introsort, der unter anderem in der Standard Template Library für C++ eingesetzt wird. Hierbei wird ein Quicksort benutzt, der im entarteten Fall auf einen Heapsort zurückfällt und somit auch im Worst-Case eine Komplexität von O(n * log(n)) aufweist.
Codebeispiele
Codebeispiele finden sich hier: https://github.com/ppasler/sorting
Es sei gesagt, dass es sich um relativ einfach Implementierungen handelt die vor allem die Funktionsweise verdeutlichen sollen und nicht jede bekannte Optimierung enthalten. Gerne mal auschecken, forken und PullRequests aufmachen.
References
| ↑1 | https://www.studytonight.com/data-structures/space-complexity-of-algorithms |
|---|---|
| ↑2 | https://www.studytonight.com/data-structures/time-complexity-of-algorithms |
| ↑3 | https://en.wikipedia.org/wiki/Big_O_notation |
| ↑4 | https://www.happycoders.eu/de/algorithmen/o-notation-zeitkomplexitaet/ |
| ↑5 | https://www.studytonight.com/data-structures/selection-sorting |
| ↑6 | https://de.wikipedia.org/wiki/Insertionsort |
| ↑7 | https://de.wikipedia.org/wiki/John_von_Neumann |
| ↑8 | https://de.wikipedia.org/wiki/Mergesort |
| ↑9 | https://docs.oracle.com/javase/8/docs/api/java/util/List.html#sort-java.util.Comparator- |
| ↑10 | https://svn.python.org/projects/python/trunk/Objects/listsort.txt |
| ↑11 | https://de.wikipedia.org/wiki/Timsort |
| ↑12 | https://de.wikipedia.org/wiki/Quicksort |
| ↑13 | https://de.wikipedia.org/wiki/Heapsort |
| ↑14 | https://de.wikipedia.org/wiki/Bubblesort |
| ↑15 | https://de.wikipedia.org/wiki/Tony_Hoare |
| ↑16 | https://de.wikipedia.org/wiki/Introsort |
